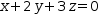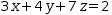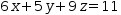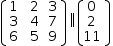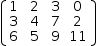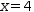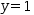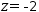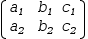3.7.1 Reduce
This transformation applies Gauss-Jordan
elimination to a matrix to transform it to reduced row echelon form.
As used in linear algebra, the coefficients and constant terms
of a system of equations can be represented by a matrix. Transforming the matrix
to reduced row-echelon form is a step toward obtaining a solution to the system of equations.
For example, given the set of equations
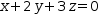 x+2⋅y+3⋅z=0,
x+2⋅y+3⋅z=0,
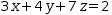 3⋅x+4⋅y+7⋅z=2
and
3⋅x+4⋅y+7⋅z=2
and
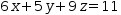 6⋅x+5⋅y+9⋅z=11, the matrix expression of coefficients
6⋅x+5⋅y+9⋅z=11, the matrix expression of coefficients
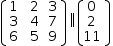 [(1, 2, 3), (3, 4, 7), (6, 5, 9)]‖[(, 0), (, 2), (, 11)]
can be simplified to
[(1, 2, 3), (3, 4, 7), (6, 5, 9)]‖[(, 0), (, 2), (, 11)]
can be simplified to
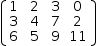 [(1, 2, 3, 0), (3, 4, 7, 2), (6, 5, 9, 11)]. Applying Reduce results in
[(1, 2, 3, 0), (3, 4, 7, 2), (6, 5, 9, 11)]. Applying Reduce results in
 [(1, 0, 0, 4), (0, 1, 0, 1), (0, 0, 1, -2)], providing a final result of
[(1, 0, 0, 4), (0, 1, 0, 1), (0, 0, 1, -2)], providing a final result of
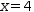 x=4,
x=4,
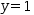 y=1
and
y=1
and
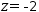 z=-2.
z=-2.
Contrast this with the techniques in §3.5.1.2, §3.6.6 and §3.7.2.
Reduction is performed symbolically. For a matrix of variables, like
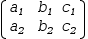 [(a_1, b_1, c_1), (a_2, b_2, c_2)],
[(a_1, b_1, c_1), (a_2, b_2, c_2)],
produces the symbolic reduction
 [(1, 0, -(b_1÷a_1)⋅(-a_2⋅c_1÷a_1+c_2)÷(-a_2⋅b_1÷a_1+b_2)+c_1÷a_1), (0, 1, (-a_2⋅c_1÷a_1+c_2)÷(-a_2⋅b_1÷a_1+b_2))].
[(1, 0, -(b_1÷a_1)⋅(-a_2⋅c_1÷a_1+c_2)÷(-a_2⋅b_1÷a_1+b_2)+c_1÷a_1), (0, 1, (-a_2⋅c_1÷a_1+c_2)÷(-a_2⋅b_1÷a_1+b_2))].